Графики Функции И Их Свойства . D(f) = r, e(f) = r. На уроке представлены различные приёмы формирования у учащихся интереса к изучению математики.
Презентация "Степенные Функции, Их Свойства И Графики" from urokimatematiki.ru
4) y наим =0, наибольшего не существует; Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график. При этом k — угловой коэффициент, b — свободный коэффициент.
Презентация "Степенные Функции, Их Свойства И Графики"
Графики функции существенно зависят от. Линейная функция у = kx + b 1. График функции у = х г изображен на рис. Графиком функции является объединение двух лучей:
Source: ppt-online.org
Логарифмы определены для a > 0 и a ≠ 1. E (y) = (−∞;0)∪ (0;+∞);;функция нечетная;функция является убывающей на промежутках xи</strong> x>0;функция не принимает ни наименьшего, ни наименьшего значения. Урок алгебры функции, их графики и свойства является обобщающим по теме. Линейная функция f (x) = kx + b. Область значений — множество (r+) всех положительных действительных чисел.
Source: www.youtube.com
Графики функции существенно зависят от значения параметра a. Понятие линейной функции линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. График функции симметричен графику функции , относительно прямой у = х(рис. Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f.
Source: videouroki.net
Сформулируем основные свойства показательной функции : Функции, их свойства и графики author: Область значений — множество (r+) всех положительных действительных чисел. 2) убывает на луче (−∞;0], возрастает на луче [0;+∞); 3) возрастает на 4) не ограничена сверху, ограничена снизу;
Source: mega-talant.com
2) убывает на луче (−∞;0], возрастает на луче [0;+∞); D (y) = (−∞;0)∪ (0;+∞);множество значений: При этом k — угловой коэффициент, b — свободный коэффициент. График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек. Графики функции существенно зависят от.
Source: urokimatematiki.ru
3) ограничена снизу, не ограничена сверху; Элементарные функции, их свойства и графики. На этом уроке мы рассматриваем степенные функции, их свойства и графики, в зависимости от основания. Y=x,x≥0 и y= −x, x≤0. Понятие линейной функции линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа.
Source: www.cleverstudents.ru
Решение показательных уравнении и неравенств Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график. Найти соответствие графика функции и его уравнения. Линейная функция 2.квадратичная функция 3.степенная функция 4.показательная функция 5.догарифмическая функция 6. Элементарные функции, их свойства и графики.
Source: ppt4web.ru
Свойства функции 1) 2) не является ни четной, ни нечетной; 4) y наим =0, наибольшего не существует; Элементарные функции, их свойства и графики. Графиком функции является прямая линия. График функции у = х г изображен на рис.
Source: urok.1sept.ru
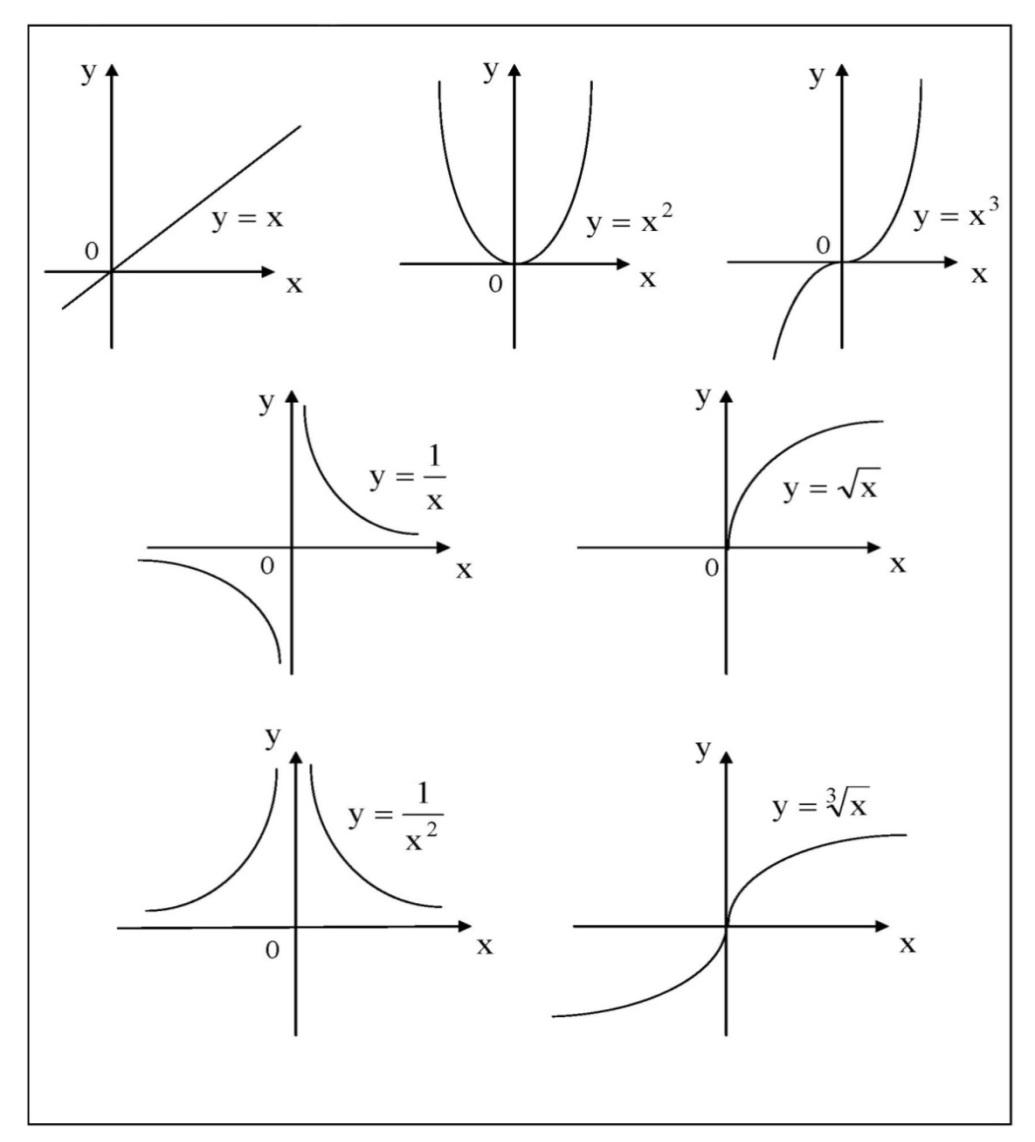
График функции y = kx + b — прямая линия. Элементарные функции, их свойства и графики. Свойства и графики некоторых функций теперь необходимо вспомнить основные свойства и графики некоторых ранее изученных функций (свойства надо представлять, но запоминать не стоит). Функции, их свойства и графики author: Степенная функция y = 𝑥− (2𝑛−1) имеет свойства:область определения:
Source: videouroki.net
Y=x,x≥0 и y= −x, x≤0. Степенная функция y = 𝑥− (2𝑛−1) имеет свойства:область определения: Свойства функции мы можем определить, глядя на график функции, и, наоборот, исследуя свойства функции мы можем построить ее график. Решение показательных уравнении и неравенств Линейная функция у = kx + b 1.
Source: znanio.ru
Y=x,x≥0 и y= −x, x≤0. Графиком функции называется совокупность всех точек на плоскости, прямоугольные координаты которых х и у удовлетворяют уравнению y=f (x). Из этих графиков очевидны характеристики и свойства этих функций: Графиком функции является прямая линия. Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,c).
Source: infourok.ru
Y=x,x≥0 и y= −x, x≤0. Линейная функция 2.квадратичная функция 3.степенная функция 4.показательная функция 5.догарифмическая функция 6. E (y) = (−∞;0)∪ (0;+∞);;функция нечетная;функция является убывающей на промежутках xи</strong> x>0;функция не принимает ни наименьшего, ни наименьшего значения. Из этих графиков очевидны характеристики и свойства этих функций: Область значений — множество (r+) всех положительных действительных чисел.
Source: www.varson.ru
Графиком функции является прямая линия. Построение графиков функции и описание их свойств (задание выполняется в группах, по карточкам) Линейная функция f (x) = kx + b. Урок алгебры функции, их графики и свойства является обобщающим по теме. График логарифмической функции для основания e (натурального логарифма) иногда называют логарифмикой.
Source: www.youtube.com
1) 2) функция не является ни четной, ни нечетной; Графики функции существенно зависят от. Здесь пример для y = 0,5x ( a = 1/2 < 1). D (y) = (−∞;0)∪ (0;+∞);множество значений: E (y) = (−∞;0)∪ (0;+∞);;функция нечетная;функция является убывающей на промежутках xи</strong> x>0;функция не принимает ни наименьшего, ни наименьшего значения.
Source: ppt-online.org
Область определения — множество (r) всех действительных чисел. Свойства функции 1) 2) не является ни четной, ни нечетной; Графиком постоянной функции является прямая, параллельная оси абсцисс и проходящая через точку с координатами (0,c). Логарифмы определены для a > 0 и a ≠ 1. 4) y наим =0, наибольшего не существует;
Source: ppt-online.org
2) убывает на луче (−∞;0], возрастает на луче [0;+∞); Графическое изображение функции имеет важное значение для её изучения. Урок алгебры функции, их графики и свойства является обобщающим по теме. 3) ограничена снизу, не ограничена сверху; Свойства функции 1) 2) не является ни четной, ни нечетной;
Source: ya-znau.ru
Область значений — множество (r+) всех положительных действительных чисел. Графическое изображение функции имеет важное значение для её изучения. У вас есть 15 минут на прохождение теста. Линейная функция 2.квадратичная функция 3.степенная функция 4.показательная функция 5.догарифмическая функция 6. Понятие линейной функции линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые.
Source: studfile.net
Можно отметить, что функции \(y = x^{2}\) и \(y = x^{4}\) обладают некоторыми сходствами. Линейная функция f (x) = kx + b. На уроке представлены различные приёмы формирования у учащихся интереса к изучению математики. Урок алгебры функции, их графики и свойства является обобщающим по теме. E (y) = (−∞;0)∪ (0;+∞);;функция нечетная;функция является убывающей на промежутках xи</strong> x>0;функция не принимает ни.
Source: www.myshared.ru
Графиком функции является прямая линия. 2) убывает на луче (−∞;0], возрастает на луче [0;+∞); График функции у = х г изображен на рис. Область значений — множество (r+) всех положительных действительных чисел. D (y) = (−∞;0)∪ (0;+∞);множество значений:
Source: infourok.ru
Графиком функции является объединение двух лучей: При этом k — угловой коэффициент, b — свободный коэффициент. Функция монотонно возрастает при k > 0 и убывает при k < 0. Графическое изображение функции имеет важное значение для её изучения. 1) 2) функция не является ни четной, ни нечетной;
Source: slide-share.ru
D(f) = r, e(f) = r. Свойства и графики некоторых функций теперь необходимо вспомнить основные свойства и графики некоторых ранее изученных функций (свойства надо представлять, но запоминать не стоит). Степенная функция y = 𝑥− (2𝑛−1) имеет свойства:область определения: Показательная и логарифмическая функции их свойства и график. На уроке представлены различные приёмы формирования у учащихся интереса к изучению математики.