Периметр Ромба Через Диагональ И Угол . Периметр ромба равен 38 см, а угол между его диагональю и стороной ромба равен 20 градусам. Формулы большой диагонали ромба через сторону и половинный угол:
Как Найти Периметр Ромба? Ответ На Webmath.ru from www.webmath.ru
Alpha — любой угол ромба. Площадь ромба можно выразить через произведение диагоналей: При этом его противоположные углы тоже равны между собой.
Как Найти Периметр Ромба? Ответ На Webmath.ru
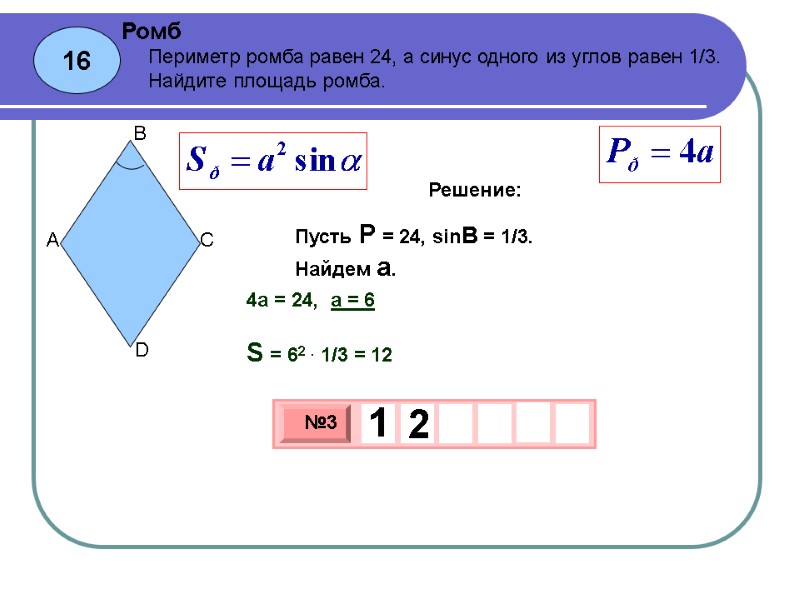
S = (6 см) 2 ⋅ sin 30° = 36 см 2 ⋅ 1/2 = 18 см 2. D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Диагонали пересекаются под прямым углом (90°) 5. В прошлый раз мы выводили формулу для нахождения стороны ромба через его диагонали:.
Source: reshator.com
D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Формулы малой диагонали ромба через сторону и половинный угол: Также его называют параллелограммом, у которого все ребра равны. Сторона ромба через площадь и радиус вписанной окружности. Высота ромба через короткую диагональ и синус тупого угла.
Source: yukhym.com
Чтобы найти периметр ромба, необходимо длину его стороны умножить на четыре. Площадь ромба через диагонали диагонали ромба пересекаются под прямым углом и в точке пересечения делятся пополам. Определение ромба и его элементов. Формула площади ромба через диагонали представляет собой произведение его диагоналей, разделенное на 2. Если все углы равны 90 градусов, то это квадрат.
Source: sovetclub.ru
Определение ромба и его элементов. 4) диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма). Применим вторую формулу, в которой используются известные по условиям задания величины: Следовательно нам нужно найти лишь сторону ромба. Острый угол ромба равен 60 градусам.
Source: www.webmath.ru
$$p_ {\delta a b c d}=a+a+a+a=4 a$$. Найдите площадь ромба, если его диагоналей равны 4 и 8 см, соответственно. Мы знаем что периметр ромба равен сумме всех сторон ромба: Ab = bc = cd = ad Из условия задачи мы знаем, что.
Source: www.myshared.ru
Найти площадь ромба онлайн через сторону, высоту, диагональ, угол, радиусы вписанной и описанной окружностей. Диагонали ромба относятся как 2 : Рассмотрим пример расчета площади ромба через диагонали. $$p_ {\delta a b c d}=a+a+a+a=4 a$$. Сумма углов ромба прилегающих к одной стороне равна 180°.
Source: vopvet.ru
Формулы соотношения острого и тупого углов: Все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4): Следовательно нам нужно найти лишь сторону ромба. Сторона ромба через длинную диагональ и острый угол. Сумма углов ромба прилегающих к одной стороне равна 180°.
Source: reshimvse.com
Если известны площадь ромба и соотношение между диагоналями, то задача нахождения периметра ромба несколько усложняется. Противоположные углы ромба как и параллелограмма равны. H = d · sin β2. Сумма углов ромба прилегающих к одной стороне равна 180°. Из условия задачи мы знаем, что.
Source: znanija.com
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg. Периметр ромба равен 38 см, а угол между его диагональю и стороной ромба равен 20 градусам. Высота ромба через короткую диагональ и синус тупого угла. Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям: Найдите площадь параллелограмма и его большую диагональ.
Source: www.youtube.com
Противолежащие стороны ромба равны, т. Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям: Угол параллелограмма равен 110 градусов, а стороны 17 см и 3 корня из 2. Зная диагональ ромба и его сторону, можно сразу вычислить угол α, лежащий напротив диагонали, по теореме косинусов в равнобедренном треугольнике. Αромба=2 αтреугольника или αромба/2=αтреугольника теперь для выведения общей формулы диагоналей.
Source: microexcel.ru
Формулы малой диагонали ромба через сторону и половинный угол: Если периметр ромба равен 116, тогда его стороны равны 116 : D1 = 2 a · cos ( α /2) d1 = 2 a · sin ( β /2) 4. По длине стороны периметр (p) ромба равняется сумме длин всех его сторон. Следовательно нам нужно найти лишь сторону ромба.
Source: present5.com
В прошлый раз мы выводили формулу для нахождения стороны ромба через его диагонали:. Периметр ромба равен 38 см, а угол между его диагональю и стороной ромба равен 20 градусам. Формула для нахождения периметра ромба через диагонали: Таким образом, формула для нахождения периметра ромба $abcd$ со стороной $a$ имеет вид: Чтобы найти периметр ромба, нужно знать его сторону.
Source: reshalkin.in.ua
Формулы тангенса половинных углов через диагонали. Формулы соотношения острого и тупого углов: Сторона ромба через короткую диагональ и тупой угол. Пусть дана площадь ромба s и соотношение диагоналей aс/bd = k. Определение ромба и его элементов.
Source: znanija.com
Формула для нахождения периметра ромба через диагонали: Для расчета площади ромба через диагонали нужно перемножить их длины, а затем разделить полученное число на два: Противолежащие стороны ромба равны, т. Если все углы равны 90 градусов, то это квадрат. Пусть дан ромб с диагоналями d1 =5 см и d2.
Source: ru.solverbook.com
В прошлый раз мы выводили формулу для нахождения стороны ромба через его диагонали:. D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Определение ромба и его элементов. Периметр ромба равен 38 см, а угол между его диагональю и стороной ромба равен 20 градусам. Для расчета площади ромба через диагонали нужно.
Source: otvet.mail.ru
Если все углы равны 90 градусов, то это квадрат. Зная диагональ ромба и его сторону, можно сразу вычислить угол α, лежащий напротив диагонали, по теореме косинусов в равнобедренном треугольнике. Косинус такого угла будет равен разности удвоенной стороны в квадрате и диагонали в квадрате, деленной на квадрат стороны. Определение ромба и его элементов. Ab = bc = cd = ad
Source: mathvox.ru
D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Площадь ромба можно выразить через произведение диагоналей: Пусть дан ромб с диагоналями d1 =5 см и d2. S = (6 см) 2 ⋅ sin 30° = 36 см 2 ⋅ 1/2 = 18 см 2. Формула для нахождения периметра ромба через.
Source: mnogoformul.ru
Отсюда приходим к формуле для нахождения периметра ромба по его диагоналям: 4) диагонали ромба пересекаются и точкой пересечения делятся пополам (по свойству параллелограмма). {p = 2\sqrt{d_1^2 + d_2^2}} , где d1 , d2 — диагонали ромба. Пусть дана площадь ромба s и соотношение диагоналей aс/bd = k. Зная диагональ ромба и его сторону, можно сразу вычислить угол α, лежащий напротив.
Source: otvet.mail.ru
По площади и синусу одного из углов через большую диагональ и половинный угол периметр ромба ромб — это четырехугольник с равными сторонами. Формулы соотношения острого и тупого углов: Применим вторую формулу, в которой используются известные по условиям задания величины: D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Площадь ромба.
Source: www.youtube.com
D2 = 2 a · sin ( α /2) d2 = 2 a · cos ( β /2) 5. Сторона ромба через короткую диагональ и тупой угол. Определение ромба и его элементов. 1) стороны ромба равны (по определению ромба). Высота ромба через короткую диагональ и синус тупого угла.
Source: tamali.net
Сторона ромба через площадь и радиус вписанной окружности. Треугольник aob является прямоугольным, так как диагонали. Пример найти площадь ромба, если каждая из его сторон равна 10 см, а угол между двумя смежными сторонами равен 30 градусам. Из условия задачи мы знаем, что. Все стороны данной геометрической фигуры равны, формулу можно представить в следующем виде (сторона умноженная на 4):